Many times, a new person joining a network (social or financial) has an impact on the members already part of the network. This kind of impacts contribute to the increase or decrease in the value of the network. These impacts in turn decides the growth or decay of the network. In this paper, we will look into some examples of such networks in current time. We will discuss many different perspectives of the network value and many laws proposed to quantify them. There have been many questions raised on the validity of these laws. hence, we will look into the issue of validity of these laws. At the end, we will discuss the different interpretation of these laws and try to put them in right perspective.
1. Introduction
When we buy some goods/service or get into a social community, we will implicitly become a part of a network. For example, buying a set-top-box(STB) connection make you a part of all the consumers having the same set-top-box connection. Even though the structure of the network and the properties of the elements (here people) is not clearly known, the group is assumed to be connected due to the common service/good or relation. The growth of such network many times depends on the value of the network when new members join them. We will look into some of the known networks and try to observe the special behavior of the networks as they grow.
Maruti Cars: Maruti is an Indian car manufacturing company. It was founded in 1981. At the time Hindustan Motors, Fiat (as Premier Automobiles Limited) like companies were present in Indian car market and selling cars. But, Maruti started becoming popular day by day. As more and more people bought Maruti cars, more and more service stations were started. These were not always started by Maruti, but sometimes were just authorized by them. As the number of Maruti cars increased, it created the opportunity to establish new service stations (due to more number of cars) and also made spares cheap due to mass production. As more number of service stations were available and spares became cheaper, people inclined towards buying more Maruti cars. Hence, whenever a person buys a Maruti car, he gets the value for the money he has as the car. But, he will also get a complementary benefit of cheap and highly accessible service. This benefit is shared between all the Maruti car owners. Hence,
Buying a Maruti Car = A Car Worth the Money Spent + Cheaper Spares + Accessible Service
The Cheaper Spares + Accessible Service part contributors to gain for all the Maruti car owners. According to the statistics of March-2011, Maruti holds 48.74% of the Indian car market share!
Migration of People to USA: America was discovered in 1492. Then it was a land of indigenous tribes. Hence, initially life was very difficult for the people coming and settling over there. As the number of adventurous and visionary people started coming to USA, the life started getting better. At some point of time, it started becoming an attraction for people looking for greater opportunities. So, people with skills to exploit the opportunities started moving to America. Due to the skilled people, there began a faster development and created more opportunities. Thus, as the number of skilled people entering USA increased, the value of the USA as a society increased. It can be given as,
New Skilled Person Entering USA = The Person Getting Opportunities Worth the Value Spent to Enter + More Opportunities + Better Lifestyle
The More Opportunities + Better Lifestyle will be the gain for all the Americans due to one person. We observe that one person entering USA increases the value of the society in USA.
Road Networks in City (More Vehicles on the Road): Assume there is a road network in a city which has no vehicles. When the first vehicle starts using it, it will have no problems like overtaking, honking, traffic jam, accidents, parking etc. But, as the number of vehicles using the same road network increases, the earlier drivers start feeling it more problematic. They will start facing all the problems mentioned above. Even the travel time increases. The cost of travel also increases due to slow driving. In other terms, whenever a new car joins the same road network, even though car owner gets the comfort of traveling a new car, he decreases the speed at which the traffic moves in the city (increases the the travel time). He also increases the cost of the travel due to the slow drive. We can represent it as,
New Vehicle Joining the City Traffic = Comfort Worth the Value of the Car to Owner +Slower Traffic + More Travel Cost
Slower Traffic + More Travel Cost is the reduction in the overall traffic system due to increase in the number of vehicles on the road.
From all the examples above, we can observe a very dominant behavior of the networks. When a new elements(person, car etc.,) is added to the network, the elements adds extra benefit or cost to all the other elements of the network. So, generically we can express this as,
New Element Joining the Network = Value Equal to Expenditure Made to Join Network + Some Benefit/Cost to all the Members of the Network
There are many such example around us which show this kind of behavior. The following are the
- People forming villages.
- People buying more Nokia phone in early 2000s.
- People buying Hero Honda vehicles in mid 90s.
- Internet.
- Arrival of IT Companies in Bangalore.
- Plantations.
- Electricity Consumption.
- Mobile Network Congestion.
In the examples seen, we have to observe that, when a new member enters a network, the network might get benefited in some aspects and might incur cost in some other aspects. So, whenever a new member joins the network, we have to look into all the aspects and take the aggregated value add to understand whether the network is getting benefited or incurring cost as a whole. If the aggregated value add is positive, network made benefitand when the aggregated value add is negative, network incurred cost.
If the network gets benefited , in aggregate, from the addition of new member, then there will be higher motivation for the people inside the network to welcome more people and also there will be higher motivation for new members to join. However, if there is absolute cost incurred by the network members and the new member when the new member joins the network, then there will be negative motivation for non members to joining the network.
2. Value of a Network
The aggregated value add is the way in which a network gets its overall value. When a new member enters the network, in case of existence of benefit, the value of the network increases and in case if the cost is incurred, the value of the network decreases. This growth of value of the network indicates a lot of future trends. Hence, many people have tried to quantify the value of the network in different aspects. The following are few interesting laws trying to quantify the value of the network.
a) Metcalfe’s Law
Robert Metcalfe is the co-inventor of Ethernet. He wanted to explain people why they should buy more and more Ethernet card. Hence, he proposed a law which asserted that the value of the Ethernet network is proportional to the square of the number of Ethernet cards connect in it. Hence, though the cost of adding new element to the network increases linearly, the value of the network due to the addition of new element increases quadratically.
The intuition for value of the network is derived from the possible number of connections in the network. If we consider a directed network with n nodes, then the maximum number of connection possible in that network is n(n-1) (if we do not consider the self loops). This is in the order of n2. Hence, it is looks intuitive that the value of the network increases quadratically. Figure 2 gives more insight about the claims of Metcalfe’s law (the image taken from wikipedia).
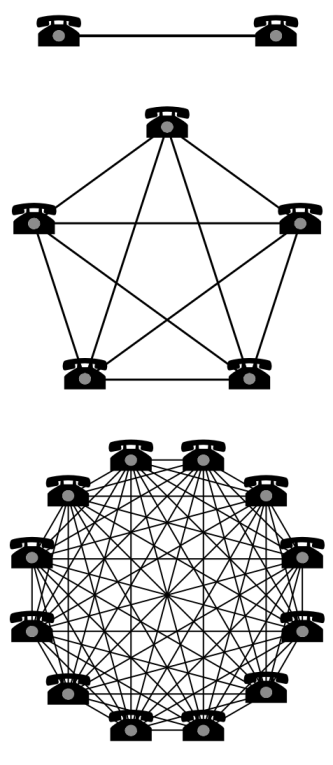
Example to explain the intuition behind the network value claims by Metcalfe’s law. The value of the network here is the “maximum number of connection possible”.
This makes network gain more value due to the addition new network element. This looks beneficial to grow the network because, for such a growth, there will always be an n, for which:
- The value of network becomes greater than cost, and
- For any value greater than n, value of network increases faster than the cost incurred, and cost starts becoming negligible.
- The network starts increasing its value in almost quadratic terms.
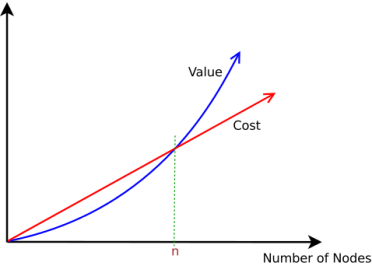
The diagrammatic representation to show that the quadratic value will always cross the linear value for some value “n”. Then the linear value starts becoming negligible.
The above figure shows this phenomenon in a graph. We can observe that once the number of elements in the network crosses n, the value of the networks becomes positive (even if it is negative earlier due to the cost of adding new nodes). After this stage, as the network grows, the linearly growing overall cost starts becoming negligible compared to the quadratically growing value of the network.
The law was later formalized by George Gilder for all the networks in 1993. He claimed that this law is not only applicable to the device networks (like Ethernet), but is also applicable to networks with users in it (economic network, business network etc).
b) Reed’s 3rd LawMetcalfe’s law became famous due to its intuitive quantification of the value of the network. In 2001, David P. Reed, an American computer scientist came up with a new law called Reed’s Law for quantifying the value of a network. He said that the Metcalfe’s law underestimates the value of the network. He claimed that the law is highly applicable for large scale networks like social networks (more on Reed’s law at:
http://en.wikipedia.org/wiki/David_P._Reed ,
http://en.wikipedia.org/wiki/Reed’s_law ). The statement of Reed’s Law goes as follows:
As networks grow, value shifts: Content (whose value is proportional to size) yields to Transactions (whose value is proportional to the square of size), and eventually Affiliation (whose value is exponential in size)
In Reed’s law,
- The meaning of the term content is the number of nodes.
- The meaning of the term affiliation is the social and business relationship.
Reed’s law tells that when a network starts building, it will have value only because of its individual members, as there are not transactions between members and no affiliations too. But, later, the members of the network get into transactions. Because of the transactions, the value of the network becomes quadratic in nature(similar to Metcalfe’s Law). Due to the transactions, the members will come together and form different communities. The real value of the network becomes exponential due to formation of such of communities.
The intuitive proof of Reed’s Law goes like this. When members start transacting, in a nmember network, the maximum number of transaction each person can do is n-1. Hence, the total number of transactions in the network will be n x (n-1), which is O(n2). Hence, Reed claims that the value of the network due to transactions is quadratic.
When the member start forming the communities, the maximum number of Group-Forming-Networks(GFC) people can form with other members is 2n – n – 1. A GFN is nothing but any community formed by the some members of the network. 2n is the cardinality of the power set of n members. We subtract n from with a naive assumption that there can not be single member communities. We subtract 1, as it represents the number of empty sets in the power set. 2n – n – 1 is in the order of O(2n). Hence, Reed claims that the value of the network due to the affiliations is exponential in nature.
c) Beckstrom’s Law
Beckstrom’s law was proposed by Rod Beckstrom in 2009. Beckstrom claims that this law can be used to evaluate any kind of network including electronic networks, social networks, supports networks and Internet. The laws states that:
The value of a network equals the net value added to each user’s transactions conducted through that network, summed over all users.
The Beckstrom’s law takes completely different look at the value getting added to the network. Instead of looking into structure and number of nodes as the input for calculating the value of the network, Beckstrom’s law looks at each transaction happening in the network (represented as an edge) as the input for calculating the value of the network. The law looks at the factor of “how valuable is the network for each user“. This is calculated by aggregating all the benefits a member gets due to the presence of the member in the network. This factor in aggregation over all the members is used to calculate the value of the complete network.
It is not that each transaction in the network adds value to the member. It is possible that due to presence of the network, the member might incur more cost. This cost is also taken care when the value of the transactions is calculated. Hence, if the member is incurring cost due to the presence of the network, the value of the network might reduce. This is a new way of looking at the value of network, which was not done by both Metcalfe’s law and Reed’s law.
To understand how value is derived from the network, let us look at an example. Assume that you wanted to buy an laptop. You visit the stores near by and understand that the minimum prize it is available for is Rs. 30000 and you decide to buy. Now, while browsing, you come across the same model of the laptop for Rs. 28000 on Flipkart. You also get to know that, they provide additional 3-years warranty free complimentary (which is worth Rs. 2000). Now, we know that by buy on-line, we will save Rs. 4000 in total. This is the value generated by us by the transaction. Similarly, the Flipkart will also gain in the transaction, say Rs.1000. Similarly, there might be many nodes in the network which will get value add. The value of the network will be the aggregate (sum) of all the gains.
Beckstrom’s law takes care of the temporal aspect of the network value. When a transaction adds value to the network, its value will not remain the same over time. As the time progresses, its values starts decaying. Hence, after some time, if there no transaction in the network then the network starts losing the value as time passes.
3. Review and Interpretation of Laws
Questioning the Validity of Metcalfe’s Law (Metcalfe’s Law is Wrong): There has been many criticism on the Metcalfe’s and Reed’s Laws. The first argument focuses on the the number of connections handled by each node in the network. The argument says that the Metcalfe’s and Reed’s Law can not be applied to quantify the value of networks involving people as the members. People have limit to the number of stable connections they can manage. Once the number of connections get saturated, the person can not get involved in any more connections. So, growth rate is not always quadratic and is restricted by the saturation of connection handling capability of people.
The other kind of argument talks about the nature of connection distribution in network. The claim is “the value of the network with n member is of the order of n log(n)”. The basis for the claim lies in the assumption that the distribution of connections follows the Zipf’s law. Hence, the connection distribution for each member for all other members looks like 1, 1⁄2 , 1⁄3 , … , 1⁄n-1. It mean that if there is observation on the connection time of a member with other members, and if the maximum connection time is normalized to 1, then other connection times will look like 1, 1⁄2, 1⁄3, … , 1⁄n-1. So the value of the network contributed by one member is 1 + 1⁄2 + 1⁄3 + … + 1⁄n-1.For infinitely big network this series converges to log(n). As there are n such member, the value of the network is n log(n).
Interpretations and Analysis of the Laws: As we saw these laws, and their criticisms, it was getting more and more evident that we are misunderstanding the laws in some conditions. We have intuitively understood that even though all these laws talk about the {value of the network}, the value is measured in different contexts for each of the laws. Hence, in this section, we will try to understand different context where these laws will be used and their different interpretations.
Interpretations of Metcalfe’s Law: Metcalfe’s law is used in the context, where we need to understand the value of the network in terms of number of connection. Here are some the observations.
- Metcalfe’s Law values the network in terms of the number of possible connections in the network. The number of possible connection is also an indication of number of possible transactions. Note that it is the upper bound of the network value. Hence, we should not misunderstand the the value of the network will always be at its maximum.
- Metcalfe’s Law is highly applicable to small network like LAN, where almost every machine is connected to every other machine. In such small networks, it may be possible that the maximum value is reached by such network.
- The law has the limitation when we try to apply this on network with people as the members. This is due to the saturation of the number of connections an individual member can handle. The law ignores the fact of probability of the connection between different members and hence ends up misleading for larger networks.
Interpretations of Reed’s Law: Reed’s law used in the context of understanding society value in the network. We interpret Reed’s law as below.
- Reed’s law talks about the value of the network being proportional to the exponent (2n) of the number of member. This means that, the value of the network found using the Reed’s law is the value in terms of the number of different groups that can be formed in the network.
- The value of the network formed puts an upper bound on the actual value of the network. Even if the the value of the network may not be equal to the value proposed by Reed’s law, it can never cross it. Hence, Reed’s law defines the boundaries of the value of the network in its own context.
- The Reed’s law is applicable in the small networks which show the tendency of heterogeneous group formations. For example, in the a small apartment society, there will be different groups like sports club, music club, drama club, trekkers etc.,. There, the value of the network might be very near to the value proposed by Reed’s law. But, when the network size increases, then value of the network will not grow exponentially. The law ignores the fact of probability of the connection between different members and hence ends up missing this point.
Interpretations of Beckstrom’s Law: Beckstrom’s Law talks about the value of a network due to the transactions in the network.
- The law rightly identifies the transactions between the members as the potential contributors to the network value.
- The law has a provision for network value to decay due to the increased cost in transactions. This makes sure that many other factors causing negative effect on the value of the networks are also considered.
- The decay of the generated value over time tells that value of the network is temporal in nature. This is a new way of looking at the value of a network. Due to the temporal nature, the value of network starts decreasing when the number of transactions in the network stop. There will be threshold value of transaction value. If this transactions do not generate this threshold value, then the value of the network starts decreasing.
- This can not capture the value added only by the presence of a member in the network. For example, presence of a film start in a commercial good network might bring many other fans to the network. These fans may in turn add value to the network. But, the law does not work in that context.
We have to understand the contexts of the applicability of the laws to understand them better. Like Moor’s law, these laws are not immutable laws as well. They are laws which indicate tendencies but are not strict in nature.
4. Conclusion
It has been observed that many networks increase or decrease in their value due to the addition of new members. This phenomena can in turn be the reason for the growth or decay of a network. Due to this kind of importance, there have been many attempts to quantify the value of a network by many people. Metcalfe, Reed and Beckstrom came up with own laws to quantify the value of a network. They looked into different aspects of the networks and tried to quantify the value of the networks in those contexts. But, it has always been misunderstood that all of them proposed the value of for a network in the same context. Metcalfe and Reed have ignored some important factors like saturation of limit of connections for individual human beings while proposing the laws. These has become a reason for lot of controversies and criticisms. But, when we keep the contexts in the view, then these laws give us lot of important properties.
REFERENCES
- Hendlera, J and Golbeck, J. Metcalfe’s Law, Web 2.0, and the Semantic Web. Web Semantics: Science, Services and Agents on the World Wide Web.
- Reed, D.P. The Law of the Pack. Harvard Business Review. 2001
- Odlyzko, A. and Tilly, B. A refutation of Metcalfe’s Law and a better estimate for the value of networks and network interconnections. Manuscript, March. 2005
- Briscoe, B. Odlyzko, A. and Tilly, Metcalfe’s Law is Wrong. IEEE Spectrum. July 2006
- Beckstrom, R. A New Model for Network Valuation. 2009






 11:15
11:15
 Juan MC Larrosa
Juan MC Larrosa













.png)





